Zadanie
V ostrouhlom trojuholníku \(ABC\) nech vektor sily má počiatok v bode \(C\) a končí v bode \(F\), ktorý je pätou výšky na strane \(AB\). Nech \(M\) je ťažisko1 strany \(AC\). Ak platí, že \(|BM| = |CF|\) a \(|\sphericalangle MBC| = |\sphericalangle FCA|\), dokážte, že trojuholník \(ABC\) je rovnostranný.
stred↩
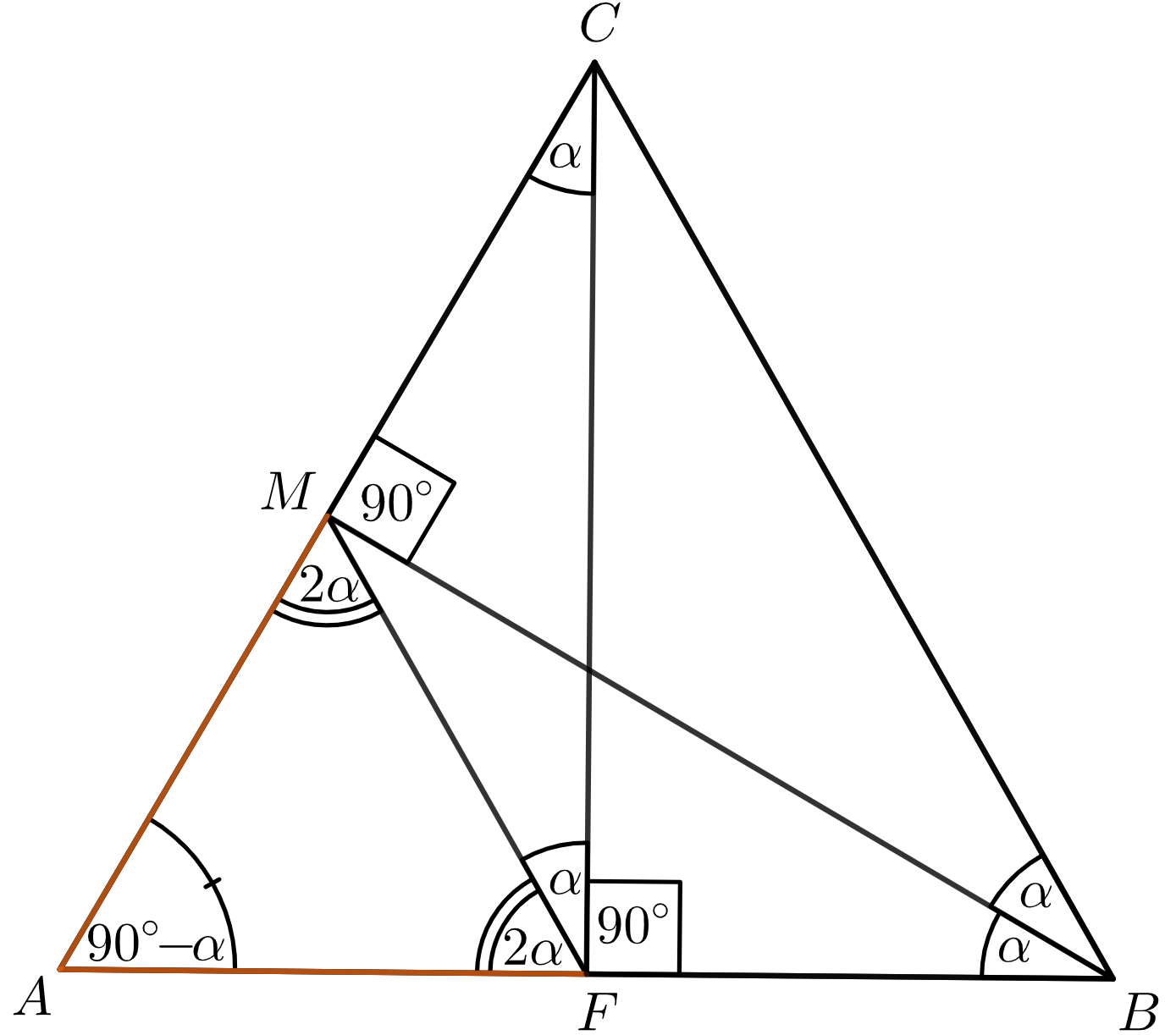
Najprv si všimnime, že \(M\) je stredom Tálesovej kružnice nad trojuholníkom \(AFC\), preto \(\lvert MC \rvert = \lvert MF \rvert\). Vďaka tomu dostávame, že \(\lvert\sphericalangle MFC\rvert=\lvert \sphericalangle MCF \rvert=\alpha\), lebo ide o rovnoramenný trojuholník. Taktiež dostávame, že \(\lvert\sphericalangle AMF\rvert=2\cdot\lvert \sphericalangle ACF \rvert=2\alpha\). Ide o stredový uhol vzhľadom k vyššie spomínanej Tálesovej kružnici. Teraz nahliadneme, že štvoruholník \(MFBC\) je tetivový (\(\lvert \sphericalangle MBC \rvert = |\sphericalangle FCA|=\alpha=\lvert \sphericalangle MFC \rvert\)). Vďaka tomu \(\lvert \sphericalangle MCF \rvert = \lvert \sphericalangle MBF \rvert= \alpha\).
Pokračujme jednoduchým pozorovaním, že \(\lvert\sphericalangle CAF\rvert=180^\circ-\lvert \sphericalangle AFC \rvert - \lvert \sphericalangle ACF \rvert=90^\circ-\alpha\), a teda \(\lvert\sphericalangle AMB\rvert=180^\circ-\lvert \sphericalangle MAB \rvert - \lvert \sphericalangle ABM \rvert=90^\circ\). Zároveň však zo zhodnosti trojuholníkov \(MAB\) a \(FAC\) podľa vety usu (pripomeňme, že \(\lvert MB \rvert = \lvert CF \rvert\)) dostávame, že \(\lvert AF \rvert = \lvert AM \rvert\). Z rovnoramennosti trojuholníka \(AMF\), dostávame, že \(\lvert\sphericalangle AMF\rvert=\lvert \sphericalangle AFM \rvert=2\alpha\), a teda \(3\alpha=90^\circ\), preto \(\alpha=30^\circ\).
Vďaka tomu \(\lvert \sphericalangle CAB \rvert = 90^\circ-30^\circ = 60^\circ = 2\cdot30^\circ=\lvert \sphericalangle ABC \rvert\), čiže trojuholník je rovnostranný.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.