9. Kirchhoffa Musíme Splniť vzorové riešenie

Na začiatok je fajn si nakresliť niekoľko takých obvodov. Ako ich nakreslíme, aby sme splnili podmienku o štvoruholníkoch? Jednoduchý spôsob je nakresliť jeden štvoruholník, potom k nemu pridať ďalší a takto postupne pridávať štvoruholníky do nášho obvodu. Keď si nakreslíme takýto obvod, tak vieme vyskúšať, či sa nám v ňom podarí nastaviť prúd podľa zadania. Len ťažko tu nájdeme nejakú prekážku, prečo by to nemalo ísť. Navyše sa nám tu ponúkne spôsob, ako taký prúd hľadať – vieme ich hľadať spolu s tým, ako náš obvod tvoríme. Ak máme len štvoruholník, tak ním vie pretekať \(1\) ampér. Druhým štvoruholníkom môžeme napr. poslať \(2\) ampére. Na miestach, kde sa tieto štvoruholníky stretnú, tak dostaneme \(1\) alebo \(3\) ampére podľa toho, či sa prúdy stretli v súhlasom smere. Ďalej sa to už komplikuje a závisí to od situácie.

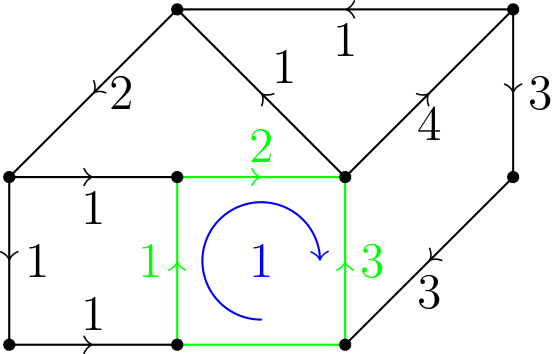
Vo všeobecnosti máme situáciu, kde máme už nejaký obvod s určenými prúdmi, napr. ako na obrázku 1. Do tohto obvodu pridáme zelený štvoruholník. Tri jeho vodiče už boli v obvode, tak nimi už tečie prúd, len jeden jeho vodič (spodný) ešte prúd nemá. Táto situácia je priaznivá, lebo napr. vo vyznačenom (modrom) smere vieme po pridanom zelenom štvoruholníku poslať \(1\) ampér, čím dostaneme prúdy podľa zadania. Avšak nie vždy to ide tak ľahko, napr. ak by sme mali v zelenom štvoruholníku dva vodiče, ktorými prechádzajú \(4\) ampére v opačných smeroch.

Úlohu vyriešime s využitím dvoch myšlienok. Najprv dovolíme dosiahnuť hodnoty prúdu vyššie ako \(4\) ampére, aby sme vedeli použiť našu ideu s posielaním vhodného prúdu do pridaného štvoruholníka. Pritom však hodnota \(5\) (spolu s \(0\)) ostane zakázaná. Môžeme sa na to aj pozerať, že zakazujeme násobky piatich. Potom ukážeme, že ak nikde nemáme prúd s hodnotou deliteľnou piatimi, tak sa vieme priveľkých hodnôt zbaviť.

V dôkaze budeme uvažovať fixný obvod \(O\). Každý jeho vodič sa nachádza v nejakom štvoruholníku – tie si označíme \(\check S_1, \check S_2, \dots, \check S_k\) postupne pre jednotlivé vodiče. Samozrejme, táto postupnosť nemusí obsahovať navzájom rôzne štvoruholníky. Matematickou indukciou ukážeme, že pre každé \(n \in \{0, 1, \dots, k\}\) platí, že obvod \(O_n\), ktorý vznikne spojením štvoruholníkov \(\check S_1, \check S_2, \dots \check S_n\) možno nastaviť prúd s hodnotami \(1\), \(2\), \(3\) a \(4\) ampére. Pre \(n = 0\) nemáme v obvode žiadne vodiče, teda tvrdenie zjavne platí. Predpokladajme teraz, že pre nejaké \(n \in \{0, 1, \dots, k - 1\}\) možno v obvode \(O_n\) nastaviť prípustný prúd. Ukážeme, že to možno spraviť aj v obvode \(O_{n+1}\).

Obvod \(O_{n+1}\) sa od obvodu \(O_n\) líši tým, že sme do neho pridali štvoruholník \(\check S_{n+1}\). Ak sa všetky vodiče štvoruholníka \(\check S_{n+1}\) už nachádzali v obvode \(O_n\), tak už nemáme čo dokazovať. V opačnom prípade niektorý vodič \(v\) štvoruholníka \(\check S_{n+1}\) nie je v obvode \(O_n\), a teda ešte nemá priradený prúd. Štvoruholníkom \(\check S_{n+1}\) prejdeme v jednom smere, čím zistíme, že vodičmi rôznymi od \(v\) pretekajú prúdy postupne \(a\), \(b\), \(c\) ampérov – tieto hodnoty môžu byť aj záporné (keď prúd tečie opačným smerom, ako vodičom prechádzame) alebo aj nulové (ak sa príslušný vodič tiež nenachádza v \(O_n\)). Teraz zvolíme také číslo \(d \in \{1, 2, 3, 4\}\), pre ktoré žiadne z čísel \(a + d\), \(b + d\), \(c + d\) nie je deliteľné piatimi – to vieme spraviť, nakoľko každé z hodnôt \(a\), \(b\), \(c\) nám vylučuje najviac jednu možnú hodnotu \(d\). Po cykle \(\check S_{n+1}\) pošleme prúd \(d\) ampérov v zvolenom smere. Tým sa dostávame do situácie, že máme nastavený prúd v obvode \(O_n\) tak, že žiadnym vodičom neprechádza prúd, ktorého veľkosť je deliteľná piatimi.

Avšak po tejto operácii môže niektorým vodičom prechádzať prúd väčší ako \(4\) ampére, presnejšie \(6\) až \(9\) ampérov. Ukážeme, že teraz sa vieme takýchto hodnôt zbaviť. Nech z uzla \(x\) do uzla \(y\) prechádza prúd veľkosti \(a \in \{6, 7, 8, 9\}\) ampérov. Teraz nájdeme orientovanú cestu z uzla \(y\) do uzla \(x\), teda cestu, na ktorej sa presúvame vodičmi vždy v smere prúdu. Nech \(M\) je množina všetkých uzlov, do ktorých sa vieme dostať z vodiča \(y\), ak dodržiavame smer prúdov. Na základe toho, ako prúdi prúd, aj pre množinu \(M\) musí platiť, že to, čo do nej vtečie, musí z nej vytiecť (pre dôkaz si dajte do rovnosti všetky prúdy vchádzajúce do uzlov v \(M\) so všetkými vychádzajúcimi prúdmi). Keďže však z \(M\) žiaden prúd nevyteká, tak nemôže ani vtekať, teda \(x\) musí byť tiež v \(M\).

Teda máme orientovanú cestu z uzla \(y\) do \(x\). Spolu s vodičom z \(x\) do \(y\) tak dostávame orientovaný cyklus \(C\) niekoľkých vodičov. Týmto cyklom \(C\) pošleme v opačnom smere prúd \(5\) ampérov. Z hodnoty \(a\) sa tak stane hodnota \(a - 5 \in \{1, 2, 3, 4\}\). To isté sa stane aj s ďalšími hodnotami medzi \(6\) a \(9\), ak ešte nejaké v cykle \(C\) boli. Zvyšné hodnoty, ktoré sú z množiny \(\{1, 2, 3, 4\}\), sa zmenia na \(\{-4, -3, -2, -1\}\), čo je v poriadku, nakoľko záporný prúd znamená opačný smer toku prúdu. Touto operáciou sa teda vieme zbaviť hodnoty väčšej ako \(4\) ampére. Ak ešte nejaká taká hodnota ostala, tak tento proces zopakujeme. Tým dosataneme hľadané prúdy aj v obvode \(O_{n+1}\), čím je náš dôkaz ukončený.

Komentáre k úlohe

Skúsení riešitelia si isto všimli, že táto úloha sa dá reprezentovať pomocou teórie grafov. V našom prípade sú vrcholy grafu uzly a hrany grafu sú vodiče. Takýto „prúd“ v grafoch sa nazýva tok. Pomocou tokov vieme reprezentovať situácie ako tečenie vody v potrubiach či pohyb áut v cestnej sieti. Avšak v týchto situáciách nám väčšinou ide o to, koľko najviac toku vieme prepraviť z jedného miesta na druhé, pričom máme zhora ohraničený tok cez jednotlivé hrany. V tejto úlohe sme však žiadne dva špeciálne vrcholy nemali. Taktiež sme tu mali pomerne netradičné obmedzenie, aby každou hranou niečo tieklo. Takýto tok sa v teórii grafov nazýva nikde-nulový tok, presnejšie nikde-nulový \(5\)-tok, keďže sme mohli používať len nenulové hodnoty menšie ako \(5\).

Nikde nulové toky nemajú až také priame uplatnenia, ale za to celkom pekne súvisia s rôznymi vlastnosťami grafov, napr. s farbeniami. Jeden taký súvis si môžete pozrieť v úlohe Korporátna Mestská Stabilita (40. ročník, 3. zimné kolo, úloha 9). Na záver ešte spomenieme, že podľa všetkého predpoklad o štvoruholníkoch je príliš silný. Čo ak by sme vyžadovali len to, že každá hrana grafu sa nachádza v nejakom cykle (teda nie nutne v cykle dĺžky \(4\))? Táto podmienka je ekvivalentná tomu, že graf nemá most, čo je taká hrana, po ktorej odstránení prestane existovať cesta medzi niektorými dvomi vrcholmi. Doterajší výskum naznačuje, že táto podmienka je postačujúca – nikomu sa nepodarilo nájsť graf, v ktorom by to nestačilo. Hypotézu o tom, že to stačí, sformuloval v roku 1954 William T. Tutte. Odvtedy sa ju nikomu nepodarilo dokázať či vyvrátiť. Význam tejto hypotézy je porovnateľný s dávnejšou hypotézou, teraz už vetou o štyroch farbách, ktorá hovorí o tom, že štáty ľubovoľnej mapy možno zafarbiť štyrmi farbami tak, aby susedné štáty mali rôzne farby. Najvýznamnejší pokrok v tomto smere dosiahol Paul Seymour, ktorý ukázal, že každý graf bez mostu pripúšťa nikde-nulový \(6\)-tok, teda tok využívajúci hodnoty \(1\), \(2\), \(3\), \(4\) a \(5\).